Mathematically derived surfaces in Revit

Introduction

Curved surfaces have been a theme of contemporary architecture for the last twenty years.

Mathematically, a curve is the result of sweeping a line through space. A line is the result of translating a point through space. Curvature is the result of the line being swept in a formula that defines a changing vector of movement.

From the engineering and construction standpoint, there are many interesting curves, such as sine wave, hyperbolic paraboloids, and conic sections. A catenary is particularly interesting because it describes the drape of a cable or chain between two points when the load is equal along the chain. It describes the form of tension structures such as a suspension bridge or the Munich Olympic Stadium by Frei Otto. Flipped over, a catenary arch is a very efficient form for compression structures, as exploited by Gaudi in the design of the Sagrada Famigilia in Barcelona. The ability to design mathematically determined surfaces is clearly a worthwhile skill.

A Point with Formulas

From the mathematical standpoint, the surface begins with a formula for a point along a line. In Revit, the first step is to create a point that can vary in height based on an input value. Open the family template for a conceptual mass. Use the Reference Point tool to add a point at the intersection of the reference planes, assuring that you use Draw on Workplane.

This first point will be our insertion point on a flat plane that defines the x and y location of the point on the surface. Name this point Location.

If you click on this point, you will see an icon for a coordinate system. Every point is placed on a workplane that defines a coordinate system and defines additional coordinate systems. By clicking the Mirrored and Flipped property check boxes, you can change the orientation of the coordinate system. By putting in a Rotation angle, you can also change the coordinate system. When you press the space bar, you toggle between a “world” coordinate system and a “local coordinate system. Before proceeding, make sure that the Mirrored and Flipped are unchecked and the angle is set to 0.

The important part of this coordinate system is the blue arrow. This defines the “normal” to the surface. The blue arrow points in the positive direction of the Z-axis in comparison to the workplane or face that hosts the point. In this case, the z axis is up compared to the world coordinates.

Two other important Properties that deserve attention are found in the Graphics section. Show Reference Planes can leave the icon for reference planes of the point always on, making it easy to notice an important point. Visible property determines whether the point is visible when the family is inserted into a another family or project. It has no impact within the family in which the point is defined; it only makes a difference after the family is loaded into another model.

Add a second point for measuring how high our surface will be by clicking anywhere on the plane. Name the second point Displacement. Also set it to be Visible.

Select the second point, then use Pick New Host, make sure Placement by Face is set, and click the Location point. An annoying dialog will appear pointing out that two points are in the same place. Just close it; we are going to move the point in a moment. The Displacement point will be controlled by the Location point using a formula.

Select the Displacement point. Because you named it, it will be easy to find as you tab through the alternative points. You will notice that it has an Offset property. This is the distance that the point is displaced from the host point (the Location). You can edit the Offset property and watch the point move up and down, always maintaining its x and y location that are determined by Location. Next, we will control Offset using a Parameter.

Open the Family Types dialog. This dialog is intended for creating types within the family that we are editing that vary in dimension or other parameter from other types in the family. This is how Revit provides a “Lumber” family that provides many types of lumber, such as a 2x4, a 1x6, or a 2x12. At this point, we are not going to create any types; we are going to create parameters that control dimensions.

Click the Add button. Fill in the fields to name the parameter h and set it to be an Instance parameter. An instance parameter can have a different value every time it is placed, while a Type parameter maintains the same value every time an instance of that type is placed.

Close the Add Parameter dialog and the Family Types dialog.

The next step is to hook the Offset of the Displacement point up to the h parameter. The h parameter, which belongs to the family, will control the value of the Offset, which belongs to the point in the family. Select the Displacement point. Next to its Offset property is an odd little button. Click on this button to open the Associate Family Parameter dialog. Click on the h parameter and close the dialog.

At this point, you will notice that you can no longer edit the value of the Offset parameter in the Properties panel. However, you can edit the value of h in the Family Types dialog. Since it controls the Offset, this will move the point up and down.

When you get this hooked up, the fun begins. The h parameter can be controlled by a formula, but you will need to create additional parameters for terms of the formula. Open the Family Types dialog and create more parameters. As you do this, note that a parameter has a “type of parameter”. This is terribly confusing because this type is completely different from the Revit family and type. Type of parameter refers to the units for the value of the parameter. Thus, a length parameters has units of feet and inches (or meters), while an angle parameter has units of degrees.

The formula for a sine wave is

• h = a * sin(p + t*f)

Where h is the height, a is the amplitude, p is the phase (or displacement of the curve from 0) and t is the time in the oscillation, and f is the frequency.

Create additional parameters with names, type of parameter, and instance or type as follows:

• a      length     Instance
• p      angle      Instance
• f      angle      Instance
• t     number  Instance

Put in the formula just as shown above into the Formula field of the h parameter. Test it by changing the parameter values and watching the point go up and down. Close the dialog and Save as p sine.rfa

This is the heart of the process of controlling a surface with formulas. Creating a line mass family and then a surface mass family requires several steps, but should seem fairly straightforward.

Line with sine

Start by making a line family. Use New Conceptual Mass. Save as line sine.rfa  Switch back to the p sine family and load it into your new line sine family.

Place a p sine at the intersection of the reference planes. You can change the parameters of p sine and watch the Displacement point go up and down.

A first step is to create a grid along a line for placing the sine wave control points. An equal grid provides for a lot of control. From the Level 1 plan, copy the horizontal reference plane 10 times. One way is to hold the ctrl key down and drag the line to a location along the vertical axis. Put a dimension on all of the planes and set it to be equal.

Dimension the first one to the second one. Use the Label control and choose Add Parameter. Name this new parameter Spacing and make it an Instance parameter. The Type of Parameter will automatically be chosen for you to be length because this is a linear dimension.

Place ten more p sine instances along the vertical reference plane. (You may need to change their parameters so that they move down onto the reference plane. Otherwise they may be invisible in the Level 1 plan.) Use the align tool to snap and lock them to the horizontal grid lines. When this is done, test it by changing the spacing. All of the reference lines should move and the points should move with them.

Now change the parameter values of each point to move them up and down. They should all have the same p, a, and f; only the t should change for each point to describe a sine wave. An easy way to set them all to have the same values is simply to select them all and change the value in the Properties panel. It will apply to all of them that are selected. The t values should vary from 0 to 9.

An elevation view shows that the sine curve has emerged. Changing the amplitude will make it more dramatic.

Nailing it together

One can go through and draw a Model Line Spline Through points through the points. This looks great, but it does not work properly. The points on the line do not attach to the controlling points. This seems very counterintuitive to me, but I can find no setting that glues them together.

However, there is a way to achieve the attachment. Metaphorically, we need a nail to hold them together.

Go back to the p sine family to draw a nail. Place another point on top of the Location. Name it Nailhead.

Open the Family Types dialog and put in a formula for hNail

• hNail = h + 1’

Close the dialog and draw a Model Line between the Displacement point and the Nailhead point. This will be a line that is visible in the line sine family. It will move up and down from the calculations for the value of h.

Turn off the visibility of the Displacement point. We want to see the model line but the Displacement point can obscure the view of the model line.

Reload the family into the line sine family.

Now it is possible to host the reference point of the spline on the bottom end point of the nail. Make sure that Placement by Face is turned on. Test it by changing the t value of the p sine that controls the nail.

Keep hosting all of the reference points. Change their t values to be the correct increment from 0 to 9 and the spline curve should reshape into sine wave.

The last step in building this line tool is to expose the parameters of the point as parameters of the line. Create the parameters for a, f, and p using the Family Types dialog, taking care to make them Instance parameters and matching the Type of Parameter to length or angle as appropriate.

You must associate the parameters in the point tool with the family parameters in the line. Select all of the p sine objects. An easy way is to use a selection set around the points and then use Filter to choose only the mass objects. Then use the Associate Family Parameter button on the p sine properties for a, f, and p. This makes it possible to change the properties of the line and control the properties of the point.

Surface

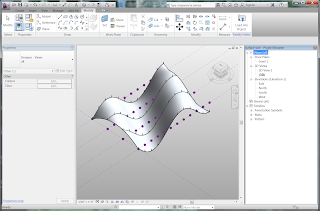With this robust mathematical line tool, it is possible to build a mathematical surface. Create a New Conceptual Mass family. Add some reference planes so that the lines can be inserted carefully. Load the line sine into the new mass family and place it several times equally spaced.

By changing the phase of each line (the p parameter), the lines each start with a different first angle.

Click each model line of the line sine objects. You may have to hover and tab to select the model line and not the entire instance. Use Create Form to produce a smooth surface.

Play with the phase, amplitude, and frequency to make new surfaces. You can also change the spacing of the grid. The forms can be very complex.

To model a different curve, simply change the formula in the point family. You can look up formulae on the Web. For example, a catenary curve equation is found at
http://classroom.synonym.com/calculate-catenary-2651.html

• y = a/2 (e^(x/a) + e^(-x/a)) 

where e is the base of the natural logarithm and is approximately 2.71828.